Writing CUDA Kernels for PyTorch

Saturday, April 20, 2024

Categories:

Machine Learning

Deep Neural Networks are compute-intensive algorithms, and if you have ever worked with PyTorch or other similar Machine Learning frameworks, you will know that training and inference of deep learning models can be accelerated dramatically by executing operations on GPUs.

With PyTorch, running on a GPU is as simple as running tensor.cuda() to move the input tensors to the GPU before performing any operation. On this page, we will take a look at what happens under the hood when you run a PyTorch operation on a GPU, and explore the basic tools and concepts you need to write your own custom GPU operations for PyTorch.

Introduction to CUDA

CUDA is a software platform developed by NVIDIA that allows us to write and execute code on NVIDIA GPUs. GPUs specialize in massively parallel computations, where a single large task is broken down into many smaller tasks that can be executed simultaneously. For this reason, the typical way we write code for CPUs (i.e. in a language like Python or C++ that executes instructions sequentially) can be quite different from how we write code for GPUs.

Writing a CUDA Kernel

We write CUDA code in C++ functions called Kernels. And although, as mentioned, operations on the GPU are executed in a highly parallel fashion across tens, hundreds, or even thousands of independent Threads, the kernel functions we write define the behavior of just a single thread.

For example, the simple and useless kernel written below prints the current Thread Index by reading the built-in threadIdx.x variable:

#include <stdio.h>

__global__ void roll_call() {
	const int threadIndex = threadIdx.x;
	printf("Thread %d here!\n", threadIndex);
}

The __global__ keyword in the function signature tells the compiler that this function is a CUDA kernel that will be invoked from the CPU and executed on the GPU. __global__ is one of the several CUDA-specific extensions to the C++ language that we will be using in our CUDA code.

To execute this kernel, we can write a main() function like the one below (note that this main() function itself is executed on the CPU like any other C++ program):

int main() {
	roll_call<<<1, 10>>>();
	cudaDeviceSynchronize();
	return 0;
}

The triple angle bracket syntax (i.e. <<<1, 10>>>) is another CUDA-specific C++ extension that is required when executing a CUDA kernel.

The first argument specifies the number of Thread Blocks to launch (we will discuss Thread Blocks in more detail later. For now, we will keep things simple by running 1 Thread Block), and the second argument specifies the number of threads per block that will be run in parallel.

So, in this example, we are launching a single Thread Block with 10 threads.

We compile this code using the nvcc compiler, which is part of the CUDA Toolkit:

nvcc roll_call.cu -o roll_call.o

Then, when we run the compiled executable, we see each thread print its index to the console:

$ ./roll_call.o
Thread 0 here!
Thread 1 here!
Thread 2 here!
Thread 3 here!
Thread 4 here!
Thread 5 here!
Thread 6 here!
Thread 7 here!
Thread 8 here!
Thread 9 here!

In the main() function above, notice that we call cudaDeviceSynchronize() after launching the kernel. This forces the execution of main() to pause until the kernel has finished executing. By default, CUDA kernels are executed asynchronously, meaning that the execution of instructions on the CPU will continue even if the GPU is still executing a kernel.

Reading and Writing Data in CUDA Kernels

A CUDA kernel’s raison d’être is nearly always to perform some computation on a set of input data, the ultimate result of which computation is eventually transferred back to the CPU, so that it can be displayed to a user, stored in a database, used as input to another computation, etc.

When writing a CUDA kernel that performs some parallelizable computation, we use the Thread Index to ensure that each thread performs a distinct piece of the overall computation.

For example, imagine that we are writing a function that accepts as input an array of integers and increments every value in the array by 1. We can write this kernel such that the thread with Thread Index i is responsible for incrementing the value at index i in the input array:

__global__ void array_increment(int* in) {
	const int threadIndex = threadIdx.x;
	in[threadIndex] = in[threadIndex] + 1;
}

It should be noted here that CUDA kernels cannot explicitly return a value, and thus must always be declared as void. To persist the results of the computation then, we must either modify the input data in-place (as in the example above), or write the results to a separate array used to store the kernel’s output. We will stick with the in-place modification approach for now, and write a main() function that uses the array_increment kernel.

Unlike the previous roll_call example where we simply launched the kernel, this time we will need to allocate memory on the GPU to store the input data, copy the input array from the host to the GPU, and finally copy the modified input array from the GPU to the host.

First, we allocate memory on the CPU using malloc and initialize an array of integers that will be used as input to the kernel:

const int arraySize = 10;

// Allocate host memory for the input array.
//
// The amount of memory allocated is equal to 
// the length of the array times the size of 
// an integer, or 10 * 4 = 40 bytes.
int* array = (int*)malloc(arraySize * sizeof(int));

// Initialize the input array with values 0, 10, 20, 30, ...
for (int i = 0; i < arraySize; i++) {
	array[i] = i*10;
}

Next, we allocate an equal amount of memory on the GPU using the cudaMalloc function, as CUDA kernels can only access data that resides in GPU memory:

// Allocate GPU memory for the input array
int* d_array;
cudaMalloc(&d_array, arraySize * sizeof(int));

After calling cudaMalloc, the d_array pointer will point to the allocated memory on the GPU. To copy the input array values from host memory (pointed to by the array variable) to the allocated section of GPU memory (pointed to by d_array), we use the cudaMemcpy function:

cudaMemcpy(
    d_array,                 // The destination memory address
    array,                   // The source memory address
    arraySize * sizeof(int), // The number of bytes to copy
    cudaMemcpyHostToDevice   // The direction of the copy
);

Finally, we launch the array_increment kernel, specifying arraySize as the number of threads (i.e. such that there is one thread launched for each element in the input array), before calling cudaMemcpy again to copy the resulting data back to host memory from GPU memory:

array_increment<<<1, arraySize>>>(d_array);

cudaMemcpy(
    array,                   // The destination memory address
    d_array,                 // The source memory address
    arraySize * sizeof(int), // The number of bytes to copy
    cudaMemcpyDeviceToHost   // The direction of the copy
);

The full main() function is shown below, with some comments and print statements thrown in for good measure:

void printArray(int* array, int arraySize) {
	printf("[");
	for (int i = 0; i < arraySize; i++) {
		printf("%d", array[i]);
		if (i < arraySize - 1) {
			printf(", ");
		}
	}
	printf("]\n");
}

int main() {
	const int arraySize = 10;
	
	// Allocate host memory for the input array
	int* array = (int*)malloc(arraySize * sizeof(int));
	
	// Initialize the input array
	for (int i = 0; i < arraySize; i++) {
		array[i] = i*10;
	}
	
	printf("Before: ");
	printArray(array, arraySize);
	
	// Allocate GPU memory for the input array
	int* d_array;
	cudaMalloc((void**)&d_array, arraySize * sizeof(int));
	
	// Copy the input array from host memory to GPU memory
	cudaMemcpy(d_array, array, arraySize * sizeof(int), cudaMemcpyHostToDevice);
	
	array_increment<<<1, arraySize>>>(d_array);
	
	// Copy the result array from GPU memory back to host memory
	cudaMemcpy(array, d_array, arraySize * sizeof(int), cudaMemcpyDeviceToHost);
	
	printf("After: ");
	printArray(array, arraySize);
	
	// Free the host and GPU memory
	free(array);
	cudaFree(d_array);
	return 0;
}

After compiling and running this code, we will see that, after executing the kernel, the values in the input array are incremented by 1:

$ ./array_increment
Before: [0, 10, 20, 30, 40, 50, 60, 70, 80, 90]
After:  [1, 11, 21, 31, 41, 51, 61, 71, 81, 91]

Note that we do not need to call cudaDeviceSynchronize() after launching the kernel in this example, as the final call to cudaMemcpy to copy the results back to host memory will force the CPU to wait until the kernel has finished executing.

Thread Blocks

You may have noticed in the previous examples that, when getting the current Thread Index, we read the value of threadIdx.x, and not simply threadIdx. This is because the threadIdx variable is of type dim3, which is essentially a 3-element tuple of integers, whose elements are accessed using its x, y, and z properties.

Thus, we can choose to represent our kernel threads as one, two, or three-dimensional blocks:

Setting the number of Threads per Thread Block to be a 2 or 3-dimensional tuple rather than a single integer, while entirely optional, can be helpful when writing kernels that deal with multi-dimensional data. As an illustration, let’s write a kernel to compute the transpose of a given square matrix.

When running this kernel, we will represent the threads as a two-dimensional block of the same size as the input matrix. This way, each thread executing our kernel will be responsible for populating one element in the output matrix.

Because the Thread Block is no longer one-dimensional, we cannot simply use threadIdx.x to uniquely identify a thread. Instead, we use both threadIdx.x and threadIdx.y, along with the Thread Block dimensions, which are stored in another dim3 type variable called blockDim:

__global__ void transpose_matrix(int* in, int* out) {
	// Select an element from the input matrix by using the
	// threadIdx x and y values. blockDim.x contains the number
	// of rows in the 2D Thread Block.
	const int threadIndex = threadIdx.x + threadIdx.y * blockDim.x;

	// Select the corresponding position in the output matrix.
	// blockDim.y contains the number of columns in the 2D Thread Block.
	const int outIdx = threadIdx.y + threadIdx.x * blockDim.y;
	out[outIdx] = in[threadIndex];
}

To launch this kernel, we first declare the Thread Block dimensions as a dim3 type, then pass this in as the number of threads per Thread Block in the triple angle brackets (<<<...>>>):

int main() {

	// Allocate host & GPU memory; Copy the input array to GPU memory
	// ...

	dim3 numThreadsPerBlock(rows, cols);
	transpose_matrix<<<1, numThreadsPerBlock>>>(d_in_matrix, d_out_matrix);

	// Release host and GPU memory
	// ...
}

Running Multiple Thread Blocks

Up until now, we have only ever launched a single Thread Block (as specified by the first value passed in the triple angle brackets) containing all of the threads that we want to run. There are many scenarios, however, where we will want or need to split our threads up into multiple Thread Blocks.

For one, there is an upper limit of 1024 threads per Thread Block. If we try to launch a kernel with more than 1024 threads in a single Thread Block, CUDA will throw an error.

The cudaGetLastError() function can be used after launching a kernel to check for errors:

int main() {
    roll_call_kernel<<<1, 1025>>>();
    
    cudaError_t err = cudaGetLastError();
    if ( err != cudaSuccess )
    {
        printf("Kernel launch error: %s\n", cudaGetErrorString(err));
        exit(-1);
    }

    cudaDeviceSynchronize();
    return 0;
}

Running this will result in the following error message, as we are not allowed to run 1025 threads in a single Thread Block:

Kernel launch error: invalid configuration argument

Splitting CUDA threads across different Thread Blocks also has implications on the performance of our kernels. To understand this, though, we need to first take a closer look at how threads and Thread Blocks are scheduled and executed on the GPU.

Streaming Multiprocessors

Nvidia GPUs are composed of one or more Streaming Multiprocessors (SMs), each of which is an individual processing unit capable of executing several threads in parallel.

The total number of Streaming Multiprocessors varies between different types of GPUs, with newer, more powerful GPUs generally having more SMs. The total number of SMs in a few popular GPU architectures is shown below:

When a CUDA kernel is launched, its threads are ultimately scheduled and executed on one or more of the GPUs Streaming Multiprocessors.

The kernel function below (a slight modification to the roll_call kernel from earlier) prints out the thread index as well as the identifier of the Streaming Multiprocessor on which the thread is running:

__global__ void sm_roll_call() {
	const int threadIndex = threadIdx.x;
	
	uint streamingMultiprocessorId;
	asm("mov.u32 %0, %smid;" : "=r"(streamingMultiprocessorId) );
	
	printf("Thread %d running on SM %d!\n", threadIndex, streamingMultiprocessorId);
}

int main() {
	sm_roll_call<<<1, 5>>>();
	cudaDeviceSynchronize();
	return 0;
}

If we launch this kernel using 1 Thread Block and 5 total threads, we will see that all 5 thread run on the same SM:

./sm_roll_call
Thread 0 running on SM 0!
Thread 1 running on SM 0!
Thread 2 running on SM 0!
Thread 3 running on SM 0!
Thread 4 running on SM 0!

In fact, all threads in the same Thread Block will always execute on the same SM. This is more evident if we modify the main function above to use multiple Thread Blocks when launching the kernel, for example, 4 Thread Blocks with 2 Threads each:

int main() {
	// Launch 4 thread blocks with 2 threads per block
	sm_roll_call<<<4, 2>>>();
	cudaDeviceSynchronize();
	return 0;
}

Thread 0 running on SM 6!
Thread 1 running on SM 6!
Thread 0 running on SM 4!
Thread 1 running on SM 4!
Thread 0 running on SM 0!
Thread 1 running on SM 0!
Thread 0 running on SM 2!
Thread 1 running on SM 2!

This time, we see that a total of 8 Threads are executed across 4 different Streaming Multiprocessors (i.e. 2 Threads per SM):

Warps

When a CUDA Kernel is launched, its Thread Blocks are first distributed among the GPU’s Streaming Multiprocessors (as seen in the last example); next, the threads within those Thread Blocks are scheduled and executed in batches of up to 32 called Warps.

Let’s create another version of our trusty old Roll Call kernel, this time to print the Warp ID as well as the Lane ID (the term Lane refers to the index of a thread within a particular warp, i.e. a value from 0 to 31) of each thread:

__global__ void warp_roll_call() {

	const int threadIndex = threadIdx.x;
	
	uint streamingMultiprocessorId;
	asm("mov.u32 %0, %smid;" : "=r"(streamingMultiprocessorId));
	
	uint warpId;
	asm volatile ("mov.u32 %0, %warpid;" : "=r"(warpId));
	
	uint laneId;
	asm volatile ("mov.u32 %0, %laneid;" : "=r"(laneId));
	
	printf("SM: %d | Warp: %d | Lane: %d | Thread %d - Here!\n", streamingMultiprocessorId, warpId, laneId, threadIndex);
}

If we run this kernel, like before, with 4 Thread Blocks of 2 threads each, we will see output like the following:

SM: 6 | Warp: 0 | Lane: 0 | Thread 0 - Here!
SM: 6 | Warp: 0 | Lane: 1 | Thread 1 - Here!
SM: 4 | Warp: 0 | Lane: 0 | Thread 0 - Here!
SM: 4 | Warp: 0 | Lane: 1 | Thread 1 - Here!
SM: 2 | Warp: 0 | Lane: 0 | Thread 0 - Here!
SM: 2 | Warp: 0 | Lane: 1 | Thread 1 - Here!
SM: 0 | Warp: 0 | Lane: 0 | Thread 0 - Here!
SM: 0 | Warp: 0 | Lane: 1 | Thread 1 - Here!

All of the Threads are executed in a single Warp (with index 0) on each SM because the Thread Blocks are all less than 32 threads. If we run a larger Thread Block (e.g. a single Thread Block with 40 threads), we see that the execution is split into 2 Warps:

SM: 0 | Warp: 1 | Lane: 0 | Thread 32 - Here!
SM: 0 | Warp: 1 | Lane: 1 | Thread 33 - Here!
SM: 0 | Warp: 1 | Lane: 2 | Thread 34 - Here!
SM: 0 | Warp: 1 | Lane: 3 | Thread 35 - Here!
SM: 0 | Warp: 1 | Lane: 4 | Thread 36 - Here!
SM: 0 | Warp: 1 | Lane: 5 | Thread 37 - Here!
SM: 0 | Warp: 1 | Lane: 6 | Thread 38 - Here!
SM: 0 | Warp: 1 | Lane: 7 | Thread 39 - Here!
SM: 0 | Warp: 0 | Lane: 0 | Thread 0 - Here!
SM: 0 | Warp: 0 | Lane: 1 | Thread 1 - Here!
SM: 0 | Warp: 0 | Lane: 2 | Thread 2 - Here!
SM: 0 | Warp: 0 | Lane: 3 | Thread 3 - Here!
SM: 0 | Warp: 0 | Lane: 4 | Thread 4 - Here!
SM: 0 | Warp: 0 | Lane: 5 | Thread 5 - Here!
SM: 0 | Warp: 0 | Lane: 6 | Thread 6 - Here!
SM: 0 | Warp: 0 | Lane: 7 | Thread 7 - Here!
SM: 0 | Warp: 0 | Lane: 8 | Thread 8 - Here!
SM: 0 | Warp: 0 | Lane: 9 | Thread 9 - Here!
SM: 0 | Warp: 0 | Lane: 10 | Thread 10 - Here!
SM: 0 | Warp: 0 | Lane: 11 | Thread 11 - Here!
SM: 0 | Warp: 0 | Lane: 12 | Thread 12 - Here!
SM: 0 | Warp: 0 | Lane: 13 | Thread 13 - Here!
SM: 0 | Warp: 0 | Lane: 14 | Thread 14 - Here!
SM: 0 | Warp: 0 | Lane: 15 | Thread 15 - Here!
SM: 0 | Warp: 0 | Lane: 16 | Thread 16 - Here!
SM: 0 | Warp: 0 | Lane: 17 | Thread 17 - Here!
SM: 0 | Warp: 0 | Lane: 18 | Thread 18 - Here!
SM: 0 | Warp: 0 | Lane: 19 | Thread 19 - Here!
SM: 0 | Warp: 0 | Lane: 20 | Thread 20 - Here!
SM: 0 | Warp: 0 | Lane: 21 | Thread 21 - Here!
SM: 0 | Warp: 0 | Lane: 22 | Thread 22 - Here!
SM: 0 | Warp: 0 | Lane: 23 | Thread 23 - Here!
SM: 0 | Warp: 0 | Lane: 24 | Thread 24 - Here!
SM: 0 | Warp: 0 | Lane: 25 | Thread 25 - Here!
SM: 0 | Warp: 0 | Lane: 26 | Thread 26 - Here!
SM: 0 | Warp: 0 | Lane: 27 | Thread 27 - Here!
SM: 0 | Warp: 0 | Lane: 28 | Thread 28 - Here!
SM: 0 | Warp: 0 | Lane: 29 | Thread 29 - Here!
SM: 0 | Warp: 0 | Lane: 30 | Thread 30 - Here!
SM: 0 | Warp: 0 | Lane: 31 | Thread 31 - Here!

Warp Schedulers

Each Streaming Multiprocessor has one or more Warp Schedulers which are responsible for choosing which Warp to execute on the SMs compute cores. For example, the A100 GPU’s Streaming Multiprocessor (shown in the diagram below taken from the NVIDIA A100 Tensor Core GPU Architecture Whitepaper) shows that this type of SM has 4 Warp Schedulers (shown in orange):

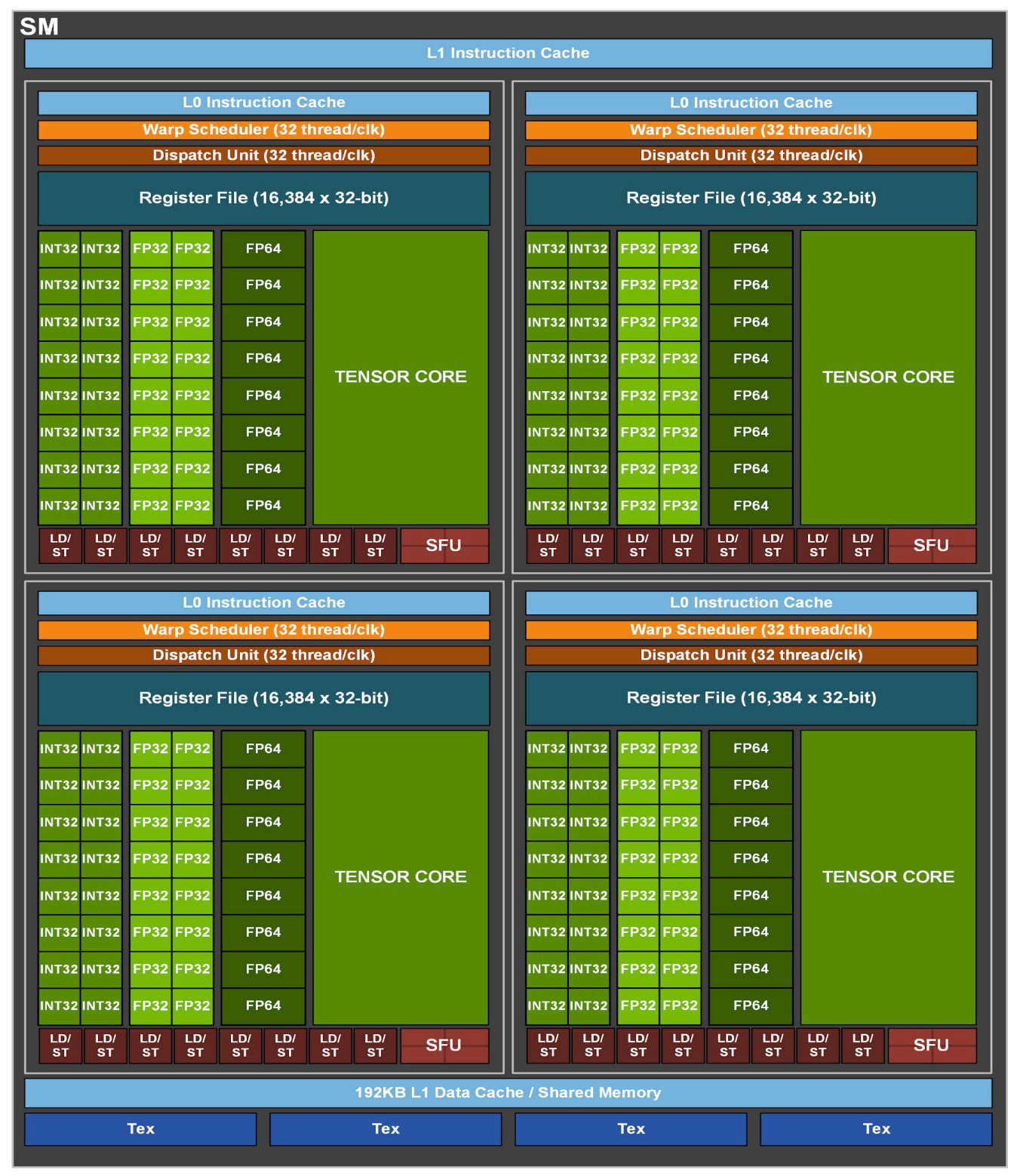
Warps do not necessarily run to completion in a linear fashion, one after the next. There are many reasons why, at any particular instant, a given Warp might not be able to execute any further: for example, the threads in the Warp may be waiting on some data to be read from memory, or they may be explicitly paused until some threads in another Warp progress (we will see an example of this when we look at __syncthreads() later on).

It is thus the task of the Warp Scheduler to decide, at each cycle, which of the available Warps should make progress. In some cases, there may not be any Warps that are able to progress further.

I find the analogy from the GTC Session CUDA Kernel Profiling using Nvidia Nsight Compute (the discussion of Warp Schedulers begins at around 17 minutes into the video) to be very helpful.

Here, the warp scheduler cycles are imagined as a conveyor belt of empty buckets. At each cycle, the Warp Scheduler must choose the next instruction from one of the available warps and place it in the bucket (i.e. the Issue Slot). If none of the Warps have an instruction that is ready to execute, then the bucket goes by empty.

CUDA Memory Hierarchy

As alluded to before, the ability to control which threads are scheduled and executed together on the same Streaming Multiprocessor has major implications for memory performance.

Broadly, there are three logical classes of memory that our kernels use to read and write data:

Memory Profiling with Nsight Compute

To get an idea of how our kernels are using these different kinds of memory, we will use, NVIDIA Nsight Compute, a profiling tool for CUDA kernels, to analyze the memory usage of a toy kernel.

Nsight Compute consists of the ncu command-line tool, which we can use to profile our CUDA kernels; and the Nsight Compute GUI, which provides a human-friendly way to view the profiling results.

Global Memory

When we allocate memory on the GPU using cudaMalloc, this space is allocated in Global Memory., the largest and slowest kind of memory available to our CUDA kernels.

Let’s write a simple kernel that uses Global Memory, and then use Nsight Compute to profile the kernel’s reads and writes.

Our kernel will compute the dot product of two input arrays, a and b, and store the result in a pointer c. (Note that this is a highly impractical kernel implementation. There is no use of the Thread Index, so all threads will perform the exact same computation. For this example though, we will only launch one thread so that our memory workload is easier to reason about).

__global__ void dot_product(float* a, float* b, float* c, int size) {
	// Compute the dot product of a and b, then store the result in c
	float sum = 0;
	for(int i = 0; i < size; i++) {
		sum += a[i] * b[i];
	}

	*c = sum;
}

We launch this kernel with a single Thread Block, a single thread, and vectorLength of 16:

int main() {
	const int vectorLength = 16;
	
	// Allocate memory for the input arrays and the output array
	// ...

	dot_product<<<1, 1>>>(d_a, d_b, d_c, vectorLength);
	
	// Copy the result back to host memory
	// ...
}

To profile this kernel we use the Nsight Compute CLI, ncu. The command below profiles the kernel and generates a report called dot_product.ncu-rep containing the results:

sudo ncu --set=full -f -o dot_product ./dot_product

When we open this report in the Nsight Compute GUI and view the Memory Workload Analysis section, a chart will be shown like the one below, which displays the different types of memory accesses made by the kernel:

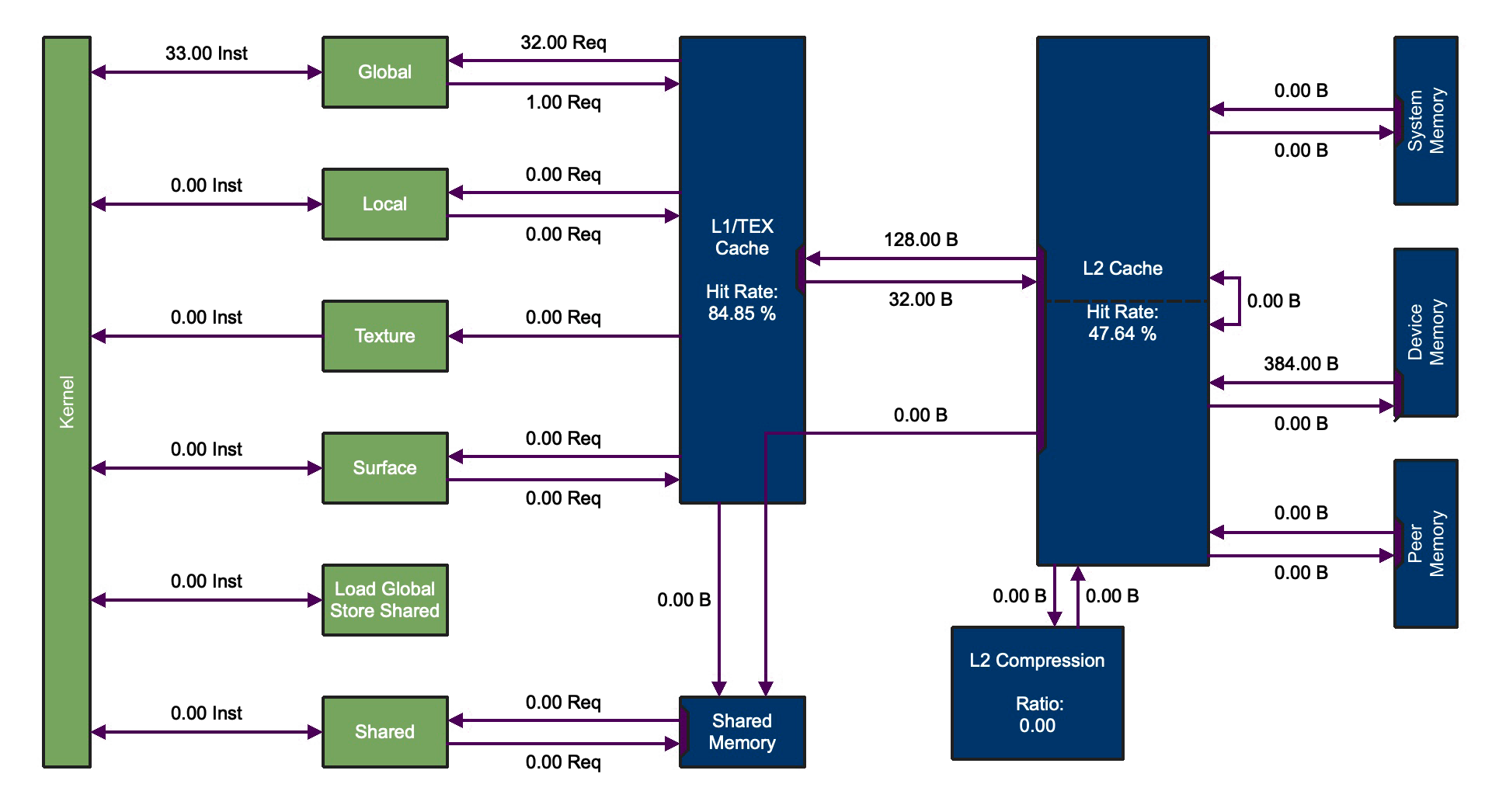
There is a lot going on in this chart, but let’s start in the upper left corner: the arrow between the green boxes Kernel and Global shows the number of instructions that read from or write to Global Memory in our kernel. In this case, there were 33 instructions (16 reads for each of the two input arrays, and 1 write for the output array).

The green boxes in the memory chart represent logical components of GPU memory with which our kernel interacts, while the blue boxes represent the physical memory spaces that underlie these logical components.

L1 and L2 Cache

Global Memory is a logical memory space that is physically backed by L1 Cache, L2 Cache, and Device Memory. When a kernel reads from Global Memory, the actual data may be retrieved from any of these three physical memory spaces.

The L1 Cache is a small, fast, and private cache that is local to each Streaming Multiprocessor. L1 Cache is checked first when a thread requests data from Global Memory; if the data is not found in L1 Cache, a read request is made to the L2 Cache (this is referred to as a Cache Miss to L2); likewise, if the data is not in L2 Cache, a read request is made to Device Memory (i.e. a Cache Miss to Device Memory).

CUDA Kernel threads read data from Global Memory in 32-byte chunks called Sectors:

We can observe this behavior in the Nsight Compute report by looking at the tables in the Memory Workload Analysis section (shown below):

The kernel made 32 read requests to L1 Cache. Of these 32 requests, 4 were Cache Misses to L2. The data read by the kernel consists of the two input arrays of size 16 each. These arrays each occupy 64 bytes of memory (16 floats * 4 bytes per float); or, in other words, 2 Sectors of 32 bytes each:

Each of these 4 sectors must be read from Device Memory before they are stored in L1 Cache, hence the 4 Cache Misses to L2. There are only 4 cache misses because each miss brings a 32-byte chunk of input data into L1 Cache; for example, the first cache miss will read the first 32 bytes (or 8 elements) of the input array a and store them in L1 Cache.

The 4 cache misses result in a total of 128 bytes read from L2 to L1 Cache, as is shown by the arrow directed from L2 Cache to L1/TEX Cache in the Memory Workload Analysis chart above.

The L2 Cache table in Nsight Compute similarly shows that 4 sectors were read from Device Memory to L2 Cache:

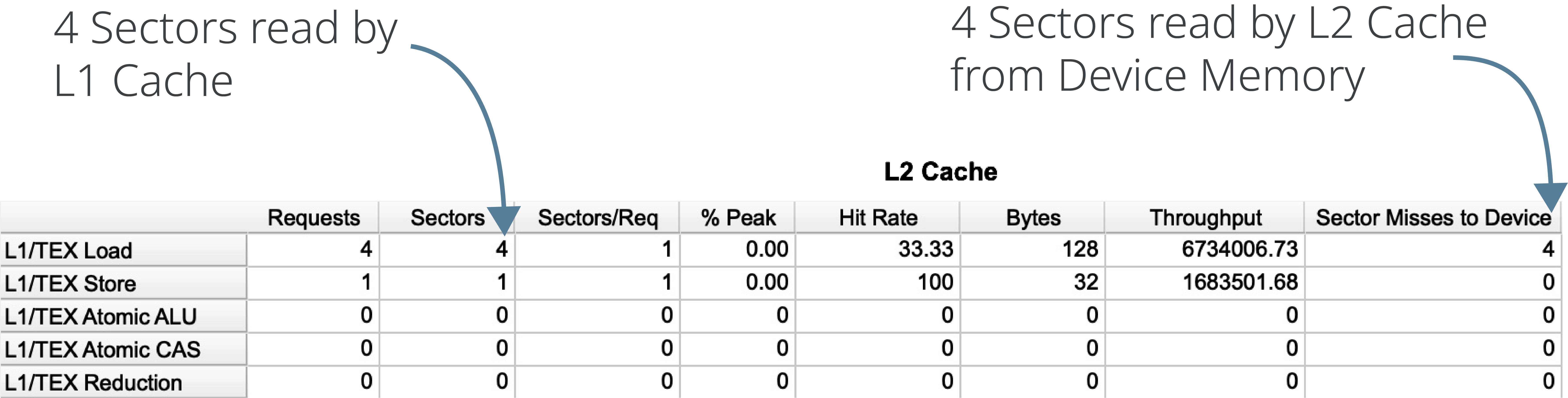
One odd thing about the statistic shown for the L2 Cache is that the Hit Rate (i.e. the number of requests from L1 which could be served without falling back to Device Memory) is 33.33%. There were 4 requests to L2 Cache and 4 Sector misses to Device Memory, so why is the Hit Rate not 0%?

The L2 Cache fetches data from Device Memory 2 Sectors at a time, so that the first 2 requests to L2 Cache result in 4 Sector misses to Device Memory. The next 2 requests, however, are for the same data that was already fetched; thus, we have 2 cache hits and 4 cache misses, or a Hit Rate of 33.33%.

These metrics are also explained in detail in the GTC Session Requests, Wavefronts, Sectors Metrics: Understanding and Optimizing Memory-Bound Kernels with Nsight Compute

Local Memory & Registers

In addition to the Global Memory that is accessible to all Streaming Multiprocessors on the GPU, each individual thread also has access to its own private Registers and Local Memory.

While both Registers and Local Memory are private to each thread, their physical locations (and as such the speed at which each is accessed) are quite different. Registers are the fastest type of memory on the GPU; generally, any scalar-type variables (ints, floats, etc.) declared in a CUDA kernel will be stored in Registers.

There is a limit to the number of registers that can be allocated to each thread and across an SM (for example, on an A100 GPU, the maximum number of registers per thread is 255).

Local variables that cannot be stored in registers (this could be because the number of registers is exhausted, or because the variable is an array whose elements are accessed dynamically at runtime) are stored in Local Memory. Local Memory is stored in the same physical locations as Global Memory and thus incurs the same latency penalty as Global Memory when accessed.

To see whether a specific variable will be stored in Registers or Local Memory, we can examine the assembly code (or PTX) generated by the nvcc compiler. The Source page in the Nsight Compute UI shows a side-by-side comparison of the original C++ code and the generated PTX assembly code.

For readability, the image below only shows a small snippet of what is displayed in Nsight Compute:

Here, we see that the line float sum = 0; in the source code corresponds to the following line in the generated PTX, which loads the value 0 into the register %f4:

mov.f32 %f4, 0f00000000;

If, however, we were to declare an array as a local variable as is shown in the C++ code below, the corresponding PTX assembly code would include the .local mnemonic, which indicates that a local variable is being loaded from Device Memory (i.e. the same location as Global Memory).

Shared Memory

The third logical memory space in the CUDA Memory Hierarchy is Shared Memory. This is a small, fast memory space that is shared between all threads in a Thread Block. Physically, Shared Memory is typically stored in the same location as the L1 Cache discussed earlier.

It is even possible to configure (to an extent) the proportion of combined L1 Cache / Shared Memory space that is dedicated to Shared Memory by setting the cudaFuncAttributePreferredSharedMemoryCarveout attribute at runtime:

cudaFuncSetAttribute(
    my_kernel,
    cudaFuncAttributePreferredSharedMemoryCarveout,
    20 // Use 20% of combined L1/Shared Memory for Shared Memory
);
my_kernel<<<num_blocks, num_threads>>>();

To allocate space in Shared Memory, we use the __shared__ keyword when declaring a variable in a CUDA kernel. Shared Memory is useful for storing data that needs to be accessed by multiple threads in a Thread Block.

All of the example kernels we have written so far have assumed that each thread executes entirely independently of the others; but to effectively use Shared Memory, we need a way to synchronize the execution of different threads (such that, for example, we can guarantee that one thread has finished writing to Shared Memory before another reads from it).

Thread Synchronization

Threads in the same Thread Block can be synchronized using the __syncthreads() function. When a thread reaches a __syncthreads() call, it will pause execution until all other threads in the Thread Block have also reached the same point.

For example, consider a kernel that applies the Softmax function to an input array. Recall that the Softmax function is used to convert a vector of real numbers into a vector of probabilities, and is given by:

$$\begin{aligned} Softmax(x_{i}) &= \frac{e^{x_{i} - x_{max}}}{\sum_{j} e^{x_{j} - x_{max}}} \end{aligned}$$

Where $ x_{max} $ is the largest value in the input vector. This function requires two full passes over the input array: one to find the maximum value, and another to compute the sum of the exponentials. A naive implementation of this kernel is shown below.

To keep things simple, we will assume that the size of the input array is a multiple of the number of threads in the Thread Block, so that each thread is responsible for computing the Softmax of multiple elements in the input array.

__global__ void softmax_kernel(float *input, float *output, int size) {
    
	// Number of threads in the Thread Block.
	// Assumes that the Thread Block is one-dimensional
	int num_threads = blockDim.x;

	// Each thread will compute the softmax of 
	// num_elements_per_thread elements
    int num_elements_per_thread = size / num_threads;
    
    int thread_index = threadIdx.x;

	// This thread will compute the softmax of elements from 
	// start_idx to end_idx in the input array
    int start_idx = thread_index * num_elements_per_thread;
    int end_idx = min(size, start_idx + num_elements_per_thread);

    // Loop over the input array to find the maximum value
    float max_val = 0.0;
    for (int i = 0; i < size; i++) {
        if (input[i] > max_val) {
            max_val = input[i];
        }
    }

    // Loop over the input array to compute sum of the exponentials
    float sum_exp = 0.0f;
    for (int i = 0; i < size; i++) {
        sum_exp += expf(input[i] - max_val);
    }

    // Store the softmax result in the output array
    for (int i = start_idx; end_idx; i++) {
        output[i] = expf(input[i] - max_val) / sum_exp;
    }
}

Example: Softmax with Shared Memory

The above implementation leads to a lot of duplicated work being performed by each Thread. Even though each thread is responsible for computing the Softmax of a unique subset of num_elements_per_thread elements, they each still loop over the entire input array twice to find the maximum value and compute the sum of the exponentials.

We can instead use Shared Memory to store the maximum value and the sum of the exponentials. We first define a new array in Shared Memory, which each thread will use to store the maximum value from its set of num_elements_per_thread elements (in other words, its local maximum value):

Once each thread has written its local maximum value to Shared Memory, we find the global maximum by looping over the set of local maximums in Shared Memory.

We can follow a similar pattern to reduce the number of redundant computations when summing the exponentials. The full kernel is shown below:

__global__ void softmax_kernel_smem(float *input, float *output, int size) {
    
    // Number of threads in the Thread Block.
	// Assumes that the Thread Block is one-dimensional
    int num_threads = blockDim.x;

    // Each thread will compute the softmax of num_elements_per_thread elements
    int num_elements_per_thread = size / num_threads;
    
    int thread_index = threadIdx.x;

    // This thread will compute the softmax of elements from start_idx to end_idx
	// in the input array
    int start_idx = thread_index * num_elements_per_thread;
    int end_idx = min(size, start_idx + num_elements_per_thread);

    // Array in shared memory to store the local max values
    __shared__ float shared_max_val[NUM_THREADS];

    float max_val = 0.0;
    for (int i = start_idx; i < end_idx; i++) {
        if (input[i] > max_val) {
            max_val = input[i];
        }
    }
    shared_max_val[thread_index] = max_val;

    // Wait for all threads to finish writing their
    // local max values to shared memory
    __syncthreads();

    for (int i = 0; i < num_threads; i++) {
        if (shared_max_val[i] > max_val) {
            max_val = shared_max_val[i];
        }
    }

    // Array in shared memory to store the local sums of 
    // the exponentials
    __shared__ float shared_sum_exp[NUM_THREADS];

    float sum_exp = 0.0f;
    for (int i = start_idx; i < end_idx; i++) {
        sum_exp += expf(input[i] - max_val);
    }
    shared_sum_exp[thread_index] = sum_exp;

    // Wait for all threads to finish writing their
    // local sums
    __syncthreads();

    for (int i = 0; i < num_threads; i++) {
        sum_exp += shared_sum_exp[i];
    }

    // Compute softmax
    for (int i = start_idx; i < end_idx; i++) {
        output[i] = expf(input[i] - max_val) / sum_exp;
    }
}

We can compare the performance of both Softmax implementations using Nsight Compute. With an input array size of 6,144 and 1,024 threads, the Shared Memory implementation takes 1.5 milliseconds to execute, while the original implementation takes 11.23 milliseconds.

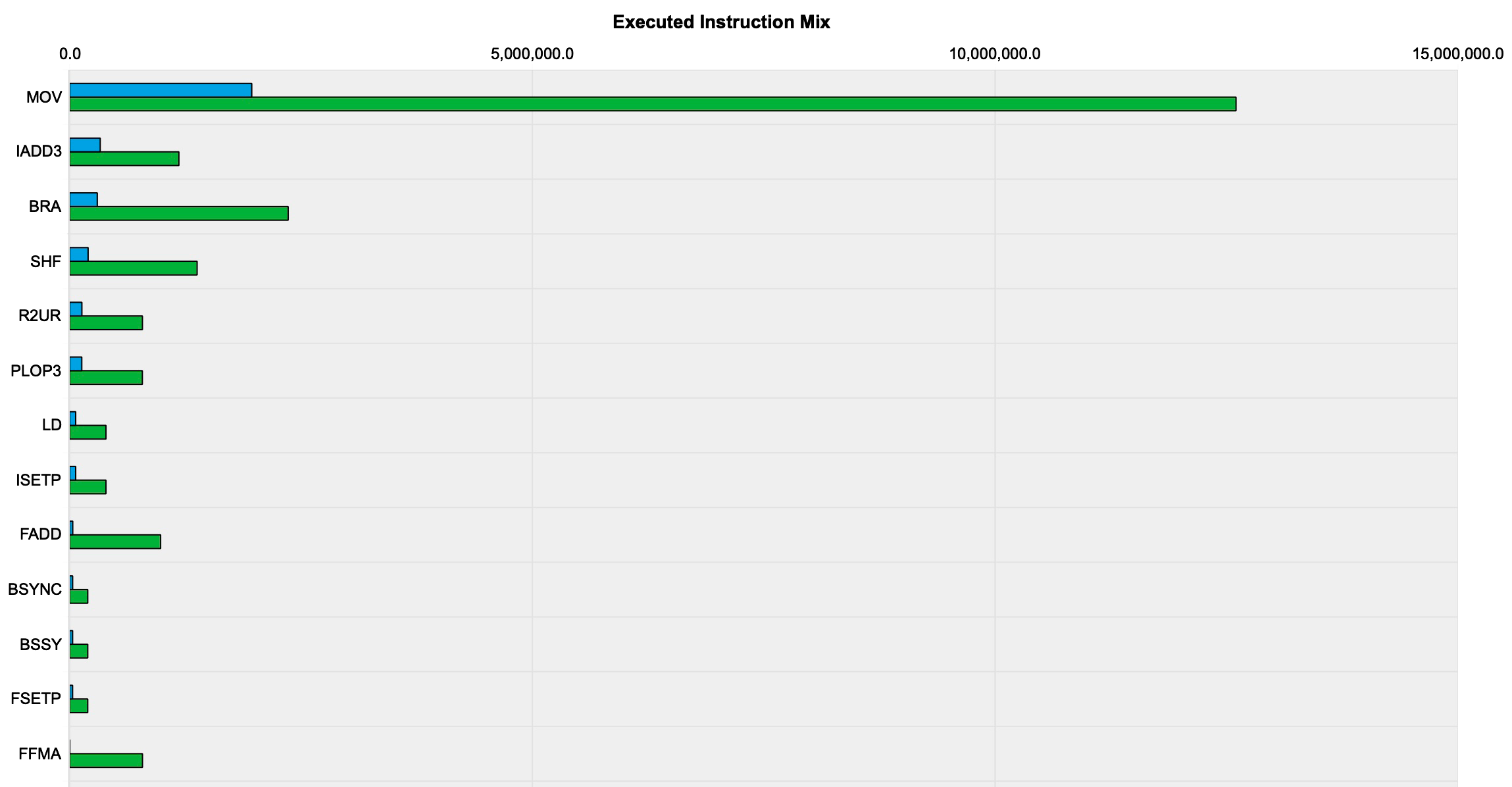
The Instruction Statistics section of the Nsight Compute report also shows that the Shared Memory implementation executes fewer instructions than the original implementation (the shared memory implementation is shown in blue below):

CUDA Basics Cheat Sheet

We covered a lot of concepts and terminology to understand the fundamentals of CUDA. Before we move on to discuss writing PyTorch operations with CUDA, feel free to take a look at the Cheat Sheet below, which sums up the core ideas and terms we have seen so far:

Writing Custom PyTorch Kernels

In this next section, we will move past basic CUDA concepts, trying out our new CUDA skills to see how to write a CUDA kernel that can be used as a custom PyTorch operation.

pybind11

We have seen how to launch CUDA kernels from C++ code using the triple angle bracket syntax (<<<...>>>), but to make a CUDA kernel that can be used easily as a PyTorch operation, we need a way to launch CUDA kernels from Python.

pybind11 is a popular library for making C++ functions and classes available within Python. On ubuntu, pybind11 can be installed with:

sudo apt-get install python3-pybind11

Let’s try out pybind11 by making the old roll_call kernel available to invoke as a Python function. First, we need to write a C++ function that calls our CUDA kernel (previously, we have been writing main() functions to launch kernels; now, we will write a simple wrapper function).

This function will be called roll_call_launcher and will be placed in the same .cu file that contains our kernel implementation:

void roll_call_launcher() {
    roll_call_kernel<<<1, 5>>>();
    cudaDeviceSynchronize();
}

Next, we create a new .cpp file and call it roll_call_binding.cpp. This file contains the special PYBIND11_MODULE declaration which allows Python code to invoke our C++ code:

#include <torch/extension.h>

// Declare the roll_call_launcher function
void roll_call_launcher();

// Write the C++ function that we will call from Python
void roll_call_binding() {
    roll_call_launcher();
}

PYBIND11_MODULE(example_kernels, m) {
  m.def(
    "roll_call", // Name of the Python function to create
    &roll_call_binding, // Corresponding C++ function to call
    "Launches the roll_call kernel" // Docstring
  );
}

Finally, we will use Python’s setuptools so that this C++ extension will be built whenever we pip install our Python code. The setup.py script is shown below:

from setuptools import setup
from torch.utils.cpp_extension import BuildExtension, CUDAExtension

__version__ = "0.0.1"

# Define the C++ extension modules
ext_modules = [
    CUDAExtension('example_kernels', [
        'csrc/roll_call/roll_call_binding.cpp',
        'csrc/roll_call/roll_call.cu',
    ])
]

setup(
    name="cuda_basics",
    version=__version__,
    ext_modules=ext_modules,
    cmdclass={"build_ext": BuildExtension}
)

Now whenever we install this library (i.e. via pip install .), an additional Python module named example_kernels will be available, making it possible to launch the roll_call kernel from Python:

$ python
Python 3.10.12 (main, Nov 20 2023, 15:14:05) [GCC 11.4.0] on linux
Type "help", "copyright", "credits" or "license" for more information.
>>> import example_kernels
>>> example_kernels.roll_call()
Thread 0 here!
Thread 1 here!
Thread 2 here!
Thread 3 here!
Thread 4 here!

There are a few different files and lots of similarly named functions and variables involved here. The visualization below hopefully provides a clearer picture of how the Python, C++, and CUDA code are wired up to make this happen:

For developers unfamiliar with C/C++, the distinction between a Function Declaration (i.e. roll_call_launcher() in roll_call_binding.cpp) and a Function Definition (roll_call_launcher() in roll_call.cu) might be a bit confusing. The function declaration defines only the name, arguments, and return type of the function; while the definition of the function defines its actual implementation.

Also, notice that the name of the Python module that ultimately gets created (in this case example_kernels) is duplicated in both setup.py and roll_call_binding.cpp. To avoid this duplication, it is a good practice to use the TORCH_EXTENSION_NAME macro from PyTorch. For example:

PYBIND11_MODULE(TORCH_EXTENSION_NAME, m) {
  m.def(
    "roll_call", // Name of the Python function to create
    &roll_call_binding, // Corresponding C++ function to call
    "Launches the roll_call kernel" // Docstring
  );
}

At build time, TORCH_EXTENSION_NAME will get replaced with whatever module name is defined in setup.py.

Using PyTorch in C++

With pybind11 now allowing us to invoke C++ and CUDA code via Python, let’s now see how we can manipulate PyTorch Tensors in a CUDA kernel.

We will revisit the array_increment kernel from before, but this time we bind this kernel to a Python function that accepts a PyTorch tensor as input. We create an array_increment_launcher function to launch the kernel.

#include <torch/extension.h>

__global__ void array_increment(int* in) {
    const int threadIndex = threadIdx.x;
    in[threadIndex] = in[threadIndex] + 1;
}

void array_increment_launcher(torch::Tensor& in, int arraySize) {
    array_increment<<<1, arraySize>>>(in.data_ptr<int>());
}

The array_increment kernel itself is unchanged from before, but notice that the array_increment_launcher function accepts as input a reference to a torch::Tensor object. To get a pointer to the underlying data stored in the tensor, we call in.data_ptr<int>()

The Python binding for this kernel is shown below:

#include <torch/extension.h>

void array_increment_launcher(torch::Tensor& in, int arraySize);

// Write the C++ function that we will call from Python
void array_increment_binding(torch::Tensor& in, int arraySize) {
    array_increment_launcher(in, arraySize);
}

PYBIND11_MODULE(TORCH_EXTENSION_NAME, m) {
  m.def(
    "array_increment", // Name of the Python function to create
    &array_increment_binding, // Corresponding C++ function to call
    "Launches the array_increment kernel" // Docstring
  );
}

We can now call this kernel with a PyTorch tensor:

>>> import torch
>>> import array_increment_kernel
>>> input = torch.tensor([1,2,3,4,5], dtype=torch.int).cuda()
>>> array_increment_kernel.array_increment(input, 5)
>>> input
tensor([2, 3, 4, 5, 6], device='cuda:0', dtype=torch.int32)

Dealing with Data Types

We often want our PyTorch operations to work with multiple different data types. The array_increment kernel, though, in its current state, only works with integer types. If we try to pass in a tensor of another type, the kernel will fail:

>>> input = torch.tensor([1,2,3,4,5], dtype=torch.float).cuda()
>>> array_increment_kernel.array_increment(input, 5)
Traceback (most recent call last):
  File "<stdin>", line 1, in <module>
RuntimeError: expected scalar type Int but found Float

To handle tensors of multiple data types, it is common to define PyTorch CUDA kernels as template functions, so that the data type of the input can be specified at runtime.

template <typename T>
__global__ void array_increment(T* in) {
    const int threadIndex = threadIdx.x;
    in[threadIndex] = in[threadIndex] + 1;
}

PyTorch even provides handy macros for invoking functions with the appropriate type based on the provided tensor. For example, the AT_DISPATCH_FLOATING_TYPES macro allows a kernel to be run on tensors of any floating point data type:

void array_increment_launcher(torch::Tensor& in, int arraySize) {
    AT_DISPATCH_FLOATING_TYPES(in.type(), "array_increment_launcher", [&]() {
        array_increment<<<1, arraySize>>>(in.data_ptr<scalar_t>());
    });
}

After rebuilding, we can test this kernel out on PyTorch tensors with different floating point data types (e.g. float32 and float64):

>>> import torch, array_increment_kernel
>>> input_f32 = torch.tensor([1,2,3,4,5], dtype=torch.float32).cuda()
>>> array_increment_kernel.array_increment(input_f32, 5)
>>> input_f32
tensor([2., 3., 4., 5., 6.], device='cuda:0')
>>> input_f64 = torch.tensor([1,2,3,4,5], dtype=torch.float64).cuda()
>>> array_increment_kernel.array_increment(input_f64, 5)
>>> input_f64
tensor([2., 3., 4., 5., 6.], device='cuda:0', dtype=torch.float64)

A number of other similar macros exist for different data types, these can be found here in the PyTorch source code: https://github.com/pytorch/pytorch/blob/main/aten/src/ATen/Dispatch.h

Wrapping Up

😮‍💨 Whew, that was a lot of work just to create a useless PyTorch operation with CUDA. Hopefully, though, this foray into the fundamentals of CUDA has helped to demystify, if only a little, the intricate world of GPU programming.

Having gone into this exercise myself with essentially no prior experience or knowledge in this space, and with a vague sense that there was something inherently spooky about writing CUDA code, I can say confidently now that it is a bit spooky, but also quite fun.

Thanks for reading 🫡